高中选文还是选理?湖南2021届新高考选科数据出炉!(附选科建议)
导读:2021湖南高考报名考生共57.49万人,除保送生、高职院校单独招生、师范生等考生外,实际考生近40.02万人,其中普通高考考生37.22万人(历史类考生16.58万人,占44.55%;物理类考生20.64万,占55.45%)。
一、单科选考分析
以下为新高考改革第三批实行3+1+2方案的省市2021届学生(刚刚结束高考的本届高三学生)的各科选考数据,从整体来看各省选科占比相对比较均衡,最受欢迎的科目是生物。
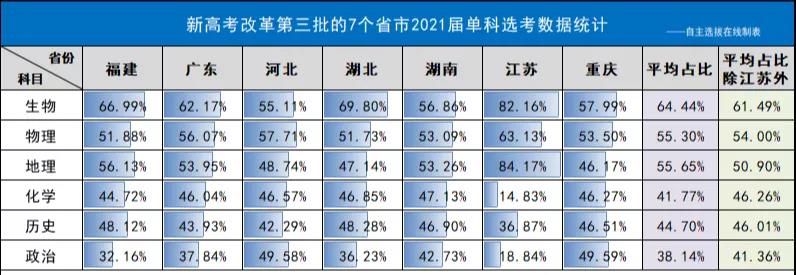
↑表格来源:自主选拔在线,非官方数据仅供参考
1、两个首选科目差距不大,偏文科人数较往年有所上涨
首先从首选的物理、历史两个科目来看,总体来说选考两科的比例很接近。而首选历史或物理一定程度上可以反映考生的偏文理程度,我们通过对比2019年其中六个省份的文科生占比情况(见下表)发现,大部分省份的偏文科比例都有所上涨。
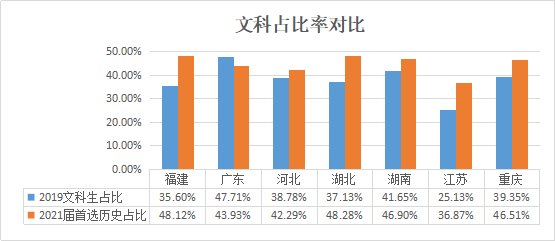
说明:表中2019文科占比数据是基于2019年各省发布的一分一段表文理人数计算而来,艺术类考生暂未计入。
2、生物成热门,政治受冷落
为方便大家直观的看出各科目选考比例,我们将这届七省选考数据转换成柱状图:
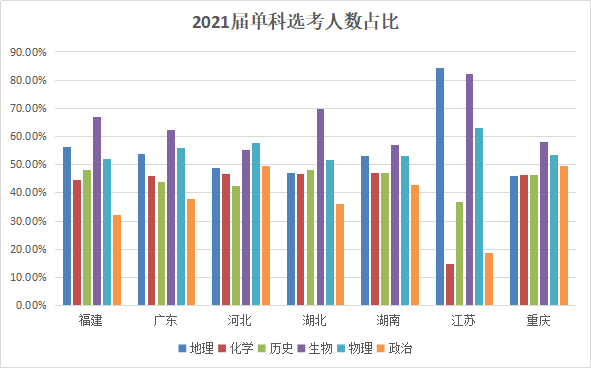
从上述图表中可以看出,生物的选考比例高居首位,紧接着就是物理和地理两门科目选考人数最多,其次就是历史、化学。而政治科目选考人数最少,这可能与政治这门学科背诵内容多、不容易拿高分的特性有关。
高中选文还是选理?湖南2021届新高考选科数据出炉!(附选科建议)
导读:2021湖南高考报名考生共57.49万人,除保送生、高职院校单独招生、师范生等考生外,实际考生近40.02万人,其中普通高考考生37.22万人(历史类考生16.58万人,占44.55%;物理类考生20.64万,占55.45%)。
一、单科选考分析
以下为新高考改革第三批实行3+1+2方案的省市2021届学生(刚刚结束高考的本届高三学生)的各科选考数据,从整体来看各省选科占比相对比较均衡,最受欢迎的科目是生物。

↑表格来源:自主选拔在线,非官方数据仅供参考
1、两个首选科目差距不大,偏文科人数较往年有所上涨
首先从首选的物理、历史两个科目来看,总体来说选考两科的比例很接近。而首选历史或物理一定程度上可以反映考生的偏文理程度,我们通过对比2019年其中六个省份的文科生占比情况(见下表)发现,大部分省份的偏文科比例都有所上涨。

说明:表中2019文科占比数据是基于2019年各省发布的一分一段表文理人数计算而来,艺术类考生暂未计入。
2、生物成热门,政治受冷落
为方便大家直观的看出各科目选考比例,我们将这届七省选考数据转换成柱状图:

从上述图表中可以看出,生物的选考比例高居首位,紧接着就是物理和地理两门科目选考人数最多,其次就是历史、化学。而政治科目选考人数最少,这可能与政治这门学科背诵内容多、不容易拿高分的特性有关。















 京公网安备11010802021790号
京公网安备11010802021790号









 学习资料
学习资料
